and the distribution of digital products.
Keep the Channel, Change the Filter: A Smarter Way to Fine-Tune AI Models
:::info Authors:
(1) Wei Chen, Purdue University, IN, USA ([email protected]);
(2) Zichen Miao, Purdue University, IN, USA ([email protected]);
(3) Qiang Qiu, Purdue University, IN, USA ([email protected]).
:::
Table of Links- Preliminary
- Methods
- Experiments
- Related Works
- Conclusion and References
- Details of Experiments
- Additional Experimental Results
\ Abstract. Efficient fine-tuning methods are critical to address the high computational and parameter complexity while adapting large pre-trained models to downstream tasks. Our study is inspired by prior research that represents each convolution filter as a linear combination of a small set of filter subspace elements, referred to as filter atoms. In this paper, we propose to fine-tune pre-trained models by adjusting only filter atoms, which are responsible for spatial-only convolution, while preserving spatially invariant channel combination knowledge in atom coefficients. In this way, we bring a new filter subspace view for model tuning. Furthermore, each filter atom can be recursively decomposed as a combination of another set of atoms, which naturally expands the number of tunable parameters in the filter subspace. By only adapting filter atoms constructed by a small number of parameters, while maintaining the rest of model parameters constant, the proposed approach is highly parameter-efficient. It effectively preserves the capabilities of pre-trained models and prevents overfitting to downstream tasks. Extensive experiments show that such a simple scheme surpasses previous tuning baselines for both discriminate and generative tasks.
\
1 IntroductionLarge models have demonstrated exceptional performance across diverse domains and tasks [2, 5, 13, 24, 45, 49, 56, 62, 66], attributing to their capability to effectively represent complex patterns and relationships [21] by pre-training on massive datasets [46 , 51 , 79]. A common strategy to adapt these large models for specific downstream tasks is fine-tuning them with full parameters. But this method presents two main challenges: (1) Adjusting a vast number of parameters for particular target tasks is computationally intensive; (2) The limited availability of target data increases the risk of overfitting [30].
\ To address these challenges, researchers have developed parameter-efficient methods [ 3 , 16 , 18 , 55 , 71 , 74] by fine-tuning the pre-trained models with only a minimal number of parameters. Among these methods, LoRA [16] fine-tunes models without altering the model architecture, becoming notably popular for
\

\ its simplicity and efficacy. However, LoRA still risks overfitting when fine-tuned on limited data and compromising the generalization capability of large models. For instance, Figure 1 illustrates that with only 5 training samples, LoRA tends to produce images that closely resemble the training data, compromising the ability for diverse image generation, compared with pre-trained models.
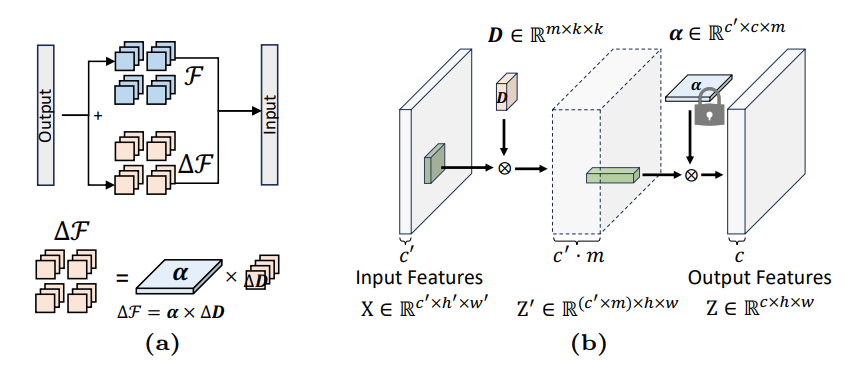
\ Motivation. To preserve the capabilities of pre-trained models when finetuning them on the downstream tasks, one prominent approach in continual learning [41, 52, 72] is to formulate convolution filters in ConvNets as a linear combination of filter atoms [29, 40, 43] and fine-tuning only filter atoms [36, 75]. Specifically, filters in each convolutional layer are decomposed over a small set of filter subspace elements, referred to as filter atoms, responsible for spatial-only convolution. Each convolutional layer is now constructed as linear combinations of filter atoms using decomposition coefficients, referred to as atom coefficients, responsible for the spatially invariant channel combination. Hypothesizing variations across tasks can be reduced by bridging spatial discrepancies in the images, we propose to calibrate the pre-trained model by solely fine-tuning the spatial-only filter atoms while preserving the spatially-invariant channel weights, i.e., atom coefficients.
\ In our work, we demonstrate that fine-tuning a large model via filter atoms is substantially effective and parameter-efficient, as filter atoms are responsible for spatial-only convolution and usually comprise only a few hundred parameters. This strategy is in harmony with task subspace modeling principles, which
\
\ suggest that task parameters occupy a low-dimensional subspace, allowing tasks to be represented as combinations of latent basis tasks [7,26,35,50,77]. We also discover that maintaining fixed atom coefficients, i.e., spatially-invariant channel mixing weights, plays a crucial role in preserving the generalization capability of pre-trained large models.
\ With a large number of parameters fixed, fine-tuning only a tiny set of parameters in filter atoms is potentially challenging to adapt to more complex tasks. We further demonstrate a simple yet effective way to expand the tunable parameters in filter subspace, without any modification on atom coefficients, by decomposing each filter atom over another set of filter atoms. This process provides an overcomplete set of filter atoms and expands the tunable parameter space, all while still requiring fewer parameters than LoRA. Additionally, we provide a simple technique to extend this method to linear layers, ensuring alignment with the characteristics in prior literature [29, 36, 40, 43]. The illustration of our method is displayed in Figure 2.
\ We demonstrate the effectiveness of our approach on both discriminative and generative tasks with ResNet50 [13], ConvNeXt [32] and Stable Diffusion [49]. We summarize our contributions as follows,
\ – We propose a method by adapting only filter subspace elements (filter atoms), with a few hundred parameters, to achieve significantly parameter-efficient fine-tuning.
\ – We observe that maintaining fixed atom coefficients plays a crucial role in preserving the generalization capability of large models.
\ – We further demonstrate a simple way to expand the number of tunable parameters in filter subspace by recursively decomposing each filter atom over another set of filter atoms, which extends the parameter space for tuning.
\ – We conduct extensive experiments demonstrating the efficacy of our approach on discriminative and generative tasks for fine-tuning large models.
\
2 Preliminary 2.1 Low-rank Adaptation for Fine-tuning\

\
2.2 Sparse Coding and Matrix Factorization\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.